U(1) Lattice Gauge Theory Simulation
This simulation arose as part of a problem set for my module Non-Perturbative Methods in Quantum Field Theory, taught by Mike Teper. It was really a very enjoyable and interesting unit; the syllabus ranged from lattice gauge theories to non-perturbatively large features of certain theories, such as solitons and instantons.
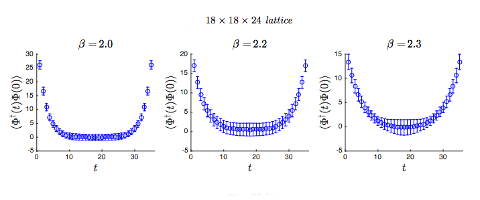
Of course representing a gauge group on a computer can be hard, so we were tasked to investigate glueball masses, plaquette averages and string tensions in U(1) scalar QED, where each element can simply be thought of as the phase of a complex number. This made life much easier.
For this assigment I implemented the Metropolis method, something that is strikingly simple but very powerful. I used only the smallest plaquettes possible to compute the action for this theory, but I pontificated in the problem set that using larger plaquettes may enable higher "resolution" when we want to investigate the exponential decay of our correlators. The done thing is actually to have plaquettes with ragged edges. The precision this affords you, it turns out, a spectrum of masses, which is really quite exciting. We weren't expected to do anything this spectacular, since our reference material was Michael Creutz's Quarks, Gluons, and Lattices, written in the days of computation where a 6x6x6x6 lattice was something of a marvel.
For this assigment I implemented the Metropolis method, something that is strikingly simple but very powerful. I first learned the Metropolis algorithm in my third year at Northwestern, where we used it to model baby systems (as if this gauge theory system is not a baby system &emdash; ha!) such as the 1-dimensional Ising magnet. It was essentially love at first sight and I knew this was how I would handle generating an ensemble of lattices. It worked fairly well, apart from a couple of correlators going negative (possibly from cumulative rounding errors; I should have known better).
I took four cracks at this simulation, first with python and then with C++. It turns out that Python was really slow when I did some very small-scale simulations just to see if parts of my project, such as generating a new lattice and extracting data from a lattice, worked. I figured that, for the sizes of ensembles that Mike wanted us to generate, my Python code would take a month to run. I didn't have a month to do this by the time I got started on it! So C++ it was!
See my third (and most successful) version of this code here, and see my write-up of the code and my results here.